Практические ограничения MFL при контроле стальных листов

Что такое MFL и для чего он нужен?

Метод поиска утечки магнитного потока (Magnetic flux leakage / MFL) широко применяется для контроля коррозии больших площадей в короткие сроки. Наиболее частное применение MFL – контроль наземных резервуаров в нефтехимической отрасли. В частности, периодический контроль дна в конструкции резервуаров для хранения продукта. На период контроля, резервуар выводится из эксплуатации и освобождается от содержимого. Это значительно удорожает время обслуживания и требует применения надежных и быстрых методов.

MFL широко используется для этой задачи, благодаря скорости его проведения и возможности по локализации дефектов на дне резервуара. В то время, как сигналы MFL часто связаны с объемом дефекта, оценка глубины дефектов, возможно, наиболее сложное и критически важное измерение, поскольку глубина дефекта непосредственно указывает на возможную близость потенциальной протечки продукта. В случае неправильной интерпретации MFL сигналов это может привести к ошибочным стратегиям ремонта и высоким финансовым издержкам. Следовательно, точное определение размера дефектов имеет решающее значение для разработки оптимальной стратегии ремонта.

В этой статье мы стремимся понять, причины возможных неправильных интерпретаций и попытаемся их минимизировать охарактеризовав влияние длины и глубины дефекта. Анализ соответствующих MFL сигналов приводит к новой многозначной эталонной схеме, с помощью которой можно уменьшить погрешность примерно на 40% при измерении глубины дефекта.

Введение

В 1988 Сондерсон [1] занимался улучшением возможности выявления дефектов коррозии на дне в конструкции наземных резервуаров. Ранее практика контроля дна резервуаров осуществлялось с помощью ультразвуковой толщинометрии. По всей площади дна резервуара в каждой точке по схеме в виде разреженной сетки производили замер толщины вручную. Природа применения ультразвуковой толщинометрии требует много времени. В [1] указывается, что при контроле резервуара диаметром 25 м с приемлемой схемой точек замеров потребуется около 1,6 миллиона измерений. Чтобы усовершенствовать подход к контролю таких объектов, Сондерсон [1] предложил метод поиска утечки магнитного потока (Magnetic flux leakage / MFL), в качестве альтернативы ультразвуку. Сондерсон отмечает, что ключевым преимуществом метода MFL является многоэлементная бесконтактная решётка из магнитных сенсоров, позволяющая производить большой охват площади контроля за один проход. Это значит, что контроль можно выполнить быстрее.

Хотя с помощью метода MFL можно проводить более быстрый контроль дна в конструкциях резервуаров, сигналы MFL, получаемые от дефектов, оказались сложны для интерпретации. Одна из причин этой сложности заключается в том, что MFL сигналы более тесно связаны с объёмом дефекта, и меньше с глубиной небольших локальных коррозионных поражений [1]. К сожалению, измерение объёма потери металла, хотя и имеет некоторую ценность, само по себе недостаточно. Например, небольшой по площади, но глубокий дефект цилиндрической формы, имеющий относительно небольшим объёмом потери металла, может оказаться гораздо более опасным, чем дефект, распространённый на большей площади с небольшой средней глубиной, имеющий больший общий объём потери металла [2].

Осознавая важность определение глубины дефекта, Сондерсон [1] предложил последовательный подход: проведение контроля на основе метода MFL в качестве поискового с дополнением ультразвуковой толщинометрии в качестве подтверждающего браковочного метода. Это позволяет получить необходимую информацию для разработки стратегии ремонта. Данный подход к контролю до сих пор считается лучшей практикой в Великобритании [3]. Однако, применение дублирующего метода увеличивает длительность контроля, а значит и простой оборудования. Это удорожает процесс контроля.

Вслед за оригинальным инструментом для поискового контроля, разработанным Сондерсоном [1], многие исследования в области MFL, включая контроль трубопроводов, были направлены на количественную оценку размеров дефектов. Конечная цель - сопоставление сигнала MFL с соответствующим по форме дефектом. Использовались различные подходы для преобразования сигналов MFL в надёжное и понятное представление о дефекте. Концепция всех подходов основывалась на реконструкции дефекта, создание образа. Эти подходы показывают компромисс между вычислительной эффективностью и точностью созданного образа профиля дефекта. Для создания образа дефекта можно выделить три основные категории: привязка к эталонному дефекту, классификация и моделирование дефекта на основе набора данных из сигналов. Количество категорий может быть расширено исходя из потребностей более точного определения профиля дефекта и проведения более эффективных расчётов.

1.1 Привязка к эталону дефекта

Привязка к эталону дефекта позволяет масштабировать уровень MFL сигналов, что позволяет оценивать размеры реальных дефектов сопоставляя их сигналы с эталоном. Несколько публикаций [4–10] проанализировали MFL сигналы в контексте определения длины, ширины, глубины дефектов и показали сложную взаимосвязь между сигналами и геометрическими параметрами дефектов. В 1995 наблюдения Чарлтона [4] позволили выработать простой подход к характеристике дефектов. Чарлтон смоделировал типовые дефекты с заданными характеристиками, и разработал на их основе справочную таблицу эталонов (также называемую калибровочные кривые), которая использовалась для масштабирования MFL сигналов. Дефекты моделируются в соответствии с условиями, которые обычно присутствуют в таких объектах, как наземные резервуары для хранения, например, нефтепродуктов. Обычно такие дефекты характеризуются естественной и равномерно растущей коррозией, когда площадь коррозионной поверхности распространяется пропорционально увеличению глубины поражения [5, 6]. Однако, точность калибровочной кривой зависит от точности моделирования и выбранных формы и объёма дефекта [1] и их способности реально предоставлять собой масштаб коррозии. Таким образом, эта простая методика ограничена, поскольку не может точно масштабировать MFL сигналы на обширных дефектах.

В 1999, взаимосвязь между MFL сигналами и длинной соответствующих дефектов изучалась Зибертом и Сазерлендом [7]. Они обнаружили, что в ограниченном диапазоне размеров, поперечное расстояние между положительным и отрицательным максимумами нормальной составляющей MFL сигнала даёт представление о длине дефекта. Более того в 2004 Хуанг и его команда [8] обнаружили, что амплитуда MFL сигнала возрастает в линейном порядке с ростом длины дефекта. В этих случаях, и длина и ширина были нормированы. Однако, по неясным причинам в исследованиях использовались длины только от 2 мм до 16 мм. Для подтверждения линейной зависимости требуется более масштабный и полный анализ.

Следующая цель – определение размеров дефектов хорошо отражена в работе Дж. Ци и его команды [9] в 2006. При исследовании ограниченного набора дефектов было обнаружено, что MFL сигнал состоит из трёх независимых функциональных величин: ширина, длина и глубина.

• Ширина: увеличение ширины дефекта может увеличивать амплитуду принимаемого MFL сигнала;

• Длина: максимум амплитуды MFL сигнала увеличивается почти линейно с увеличением длины дефекта. Это согласуется с выводами Хуанга и его команды [8] в 2004. Однако, команда Дж. Ци [9] продвинулась больше в исследованиях. Они обнаружили, что амплитуда MFL сигнала увеличивается с увеличением длины дефекта до 30 мм, а после свыше 30 мм MFL сигнал становиться стабильным.

• Глубина: в 2006 команда Дж. Ци [9] обнаружила, что это максимально критическая величина дефекта. И её труднее всего определить, так как амплитуда MFL сигнала: 1. имеет тенденцию увеличиваться нелинейно относительно увеличения глубины дефекта. 2. колеблется в нелинейном порядке, когда ширина и длина дефекта переменчивы, а глубина дефекта постоянна. Это и затрудняет определение глубины дефекта по амплитуде MFL сигнала.

Совсем недавно, в 2010 году, предпринимались дальнейшие попытки по улучшению возможности определения глубины дефектов. Над этим работал Саха и его команда [10]. При исследованиях процесса контроля трубопроводов, команда Сахи обнаружила более лучший способ определения глубины дефекта. Для этого учитывалось влияние ширины дефекта. В публикации [10] показано, что оценка глубины дефекта очень зависит от ширины дефекта. Правильно измеренная ширина дефекта важна для точного измерения глубины дефекта. Хотя такая зависимость наблюдалась ранее командой исследователей Дж. Ци [9], команда Сахи демонстрирует любопытный подход к определению ширины дефекта. Они использовали только радиальную (Y) составляющую MFL сигнала, получаемый многоэлементной решёткой из магнитных сенсоров. Вместе с определением длины дефекта команда Сахи предлагает отношение второго порядка для определения глубины дефекта. Однако, предложенная функция имеет ограничения, так как это преимущественно линейная функция длины/ширины [10]. А линейная функция противоречит нелинейной зависимости, описанной командой исследователей Дж. Ци [9].

Хотя подход с использованием опорных значений в его нынешнем виде не обеспечивал точного определения размеров дефекта, эффективность подхода была полезна с точки зрения немедленного измерения дефектов. Одним из возможных способов повышения точности определения геометрических размеров дефекта являлась классификация, вторая общая категория анализа MFL сигналов.

1.2 Классификация

Классификация опирается на характеристики, полученных из набора признаков в MFL сигналах. Признаки обычно статистически сравниваются с набором заранее определенных опорных моделей. Классификация состоит из двух необходимых этапов: подготовка и испытание. Применительно к обоим признакам, основанным, например, на вышеупомянутых геометрических размерах или посредством комплексных средств [11]. Компромиссы подготовки моделей по известным классам, см., например, [12]. Этап испытания – сам по себе процесс классификации, т.е. метод оценки, который может быть основан, например, на нейронных сетях [13] или машинном обучении [14, 15]. Можно отметить, что публикации, например, [11] склонны сосредотачиваться на улучшении процесса извлечения признаков дефекта для классификации на их основе, тогда как стандартные и легкодоступные подходы классификации основаны на вычислении вероятной категории дефекта.

При использовании MFL метода классификация применяется в двух различных путях:

1. Разделить дефекты по общим совокупностям, например, цилиндрические, конусовидные или относительно крупные очаги коррозии, напоминающие в профиле озеро, предложенные Рамиресом [14].

2. Создание образа дефекта на основе классификации по его размерам [16]. Опубликованные результаты в [16] по созданию образа дефектов на основе их классификации успешно продемонстрирована, с точностью измерений до 99%, но эти результаты основаны на отобранном ограниченном наборе смоделированных дефектов.

1.3 Обратное моделирование

Третья категория MFL анализа это обратное моделирование. Цель подхода обратного моделирования - обеспечить идеальное решение: создание детального образа профиля дефекта на основе MFL сигнала этого дефекта. Этот подход считается потенциально мощным средством обнаружения и определения характеристик дефектов при анализе MFL данных [17]; мнение, выраженное и другими публикациями [18–20].

Базовый принцип обратного моделирования — это многократное подгонка предварительной модели до получения плоскости профиля дефекта. Производится сравнение теоретически рассчитанной предварительной модели с соответствующим неизвестным (сырым) MFL сигналом. Если моделируемый и сырой сигналы MFL не похожи, параметры предварительной модели адаптируются в попытке приблизиться к реальной плоскости профиля дефекта. Цикл многократно повторяется до тех пор, пока рассчитанный и сырой сигналы не будут соотнесены между собой по определенным пользователем критериям. Подход с многократным повторением подгонки предварительной модели представляет собой точное, но дорогостоящее в вычислительном отношении решение [18].

Много текущих исследований обратного моделирования преследуют цель улучшить вычислительную эффективность предварительной модели при одновременном сохранением точности созданного образа дефекта. В настоящее время и в связи с итеративным (процессом многократно повторяющейся подгонки) характером обратного моделирования, требования, предъявляемые к компьютерам, делают их (компьютеры) потенциально очень дорогими, невозможным их использования в полевых и неблагоприятных условиях. При этом время является важным экономических фактором. Если бы можно было разработать более эффективный вычислительный процесс, тогда обратное моделирование было бы многообещающим подходом. Возможный путь к большей вычислительной эффективности в использовании обратного моделирования с поддержкой относительно высокой точности определения профиля дефекта это применение «фильтра частиц» на этапе готовой элементной модели [21]. Другие попытки повысить эффективность обратного моделирования включая замену стохастического моделирования в форме классификаторов нейронных сетей [16, 22], вейлетов (математических функций, позволяющих анализировать различные частотные компоненты данных) [23] и статистические классификаторы [24]. Можно утверждать, что обратное моделирование, по-видимому, имеет светлое будущее, но нам необходимо разработать лучший подход в сочетании с портативными технологиями завтрашнего дня.

В этой статье мы отказываемся от продвинутого и пока еще нежизнеспособного подхода - обратное моделирование - и предлагаем улучшенный, в части точности, подход – «привязки дефекта». Из MFL сигнала извлекается информация, которая позволяет определить длину и глубину соответствующих дефектов.

Получение сигнала и формы дефектов

Базовые принципы контроля ферромагнитных объектов с помощью MFL метода в первую очередь включают подходящее насыщение магнитным полем локальной зоны контроля. В непосредственной близости от дефекта сопротивление наведенному магнитному полю увеличивается и, если оно (сопротивление) достаточно высоко, наведённое магнитное поле отклоняется из-за отсутствия металла на пути прохождения поля. Часть магнитного поля отклоняется, огибая дефект в остаточном металле, а другая часть поля выталкивается («вытекает») за пределы металла. Объём вытекшего за пределы металла магнитного поля соотносят с пропорциональным объёмом дефекта [1], измерение производится специальным магнитным сенсором, который размещается на сканере у поверхности зоны контроля.

Для выполнения быстрого контроля дна конструкции резервуара, ось решётки из магнитных сенсоров располагают перпендикулярно к направлению сканирования, чтобы можно было захватить максимальную зону контроля. В этой работе MFL сигналы рассматриваются так, как если бы они были получены одним магнитным сенсором и были сгенерированы с помощью магнитостатического двухмерного моделирования конечной элементной модели.

Предусмотрено однородное магнитное поле с заранее определенной силой в 2Тл, которая позволяет получить подходящее насыщение стальной пластины толщиной 6 мм. Все MFL сигналы в этой статье получены при зазоре 3,8 мм между поверхностью образца и магнитным сенсором, в Y-направлении векторного поля магнитной индукции B^→ (где B^→ = (B_x, B_y, B_z)) в равноудалённых точках вдоль поверхности образцов. Учитываются только плоскодонные дефекты, так как это позволяет легко и независимо менять глубину и длину дефектов.

Влияние характеристик дефекта на MFL сигнал

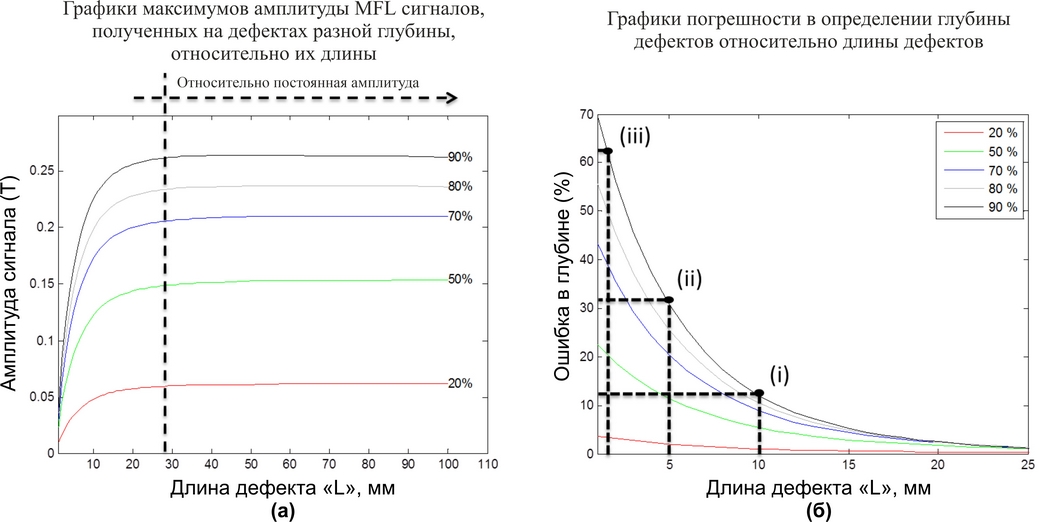
Рисунок 1(а). Пять графиков показывают максимумы амплитуд MFL сигналов от плоскодонных дефектов с глубинами: 20%, 50%, 70%, 80% и 90%, в зависимости от их длины дефекта L = от 1мм до 100мм.

Рисунок 1(б). Потенциальная погрешность в определении глубины методом MFL от истинного значения глубины дефекта, в зависимости от длины дефекта L. Наивысший уровень погрешности наблюдается в дефектах небольшой длины. Наименьшая погрешность (близкая к нулю) – у дефекта с максимальной длиной.

На Рисунке 1(а) представлены максимумы значений амплитуды MFL сигналов от дефектов, в зависимости от длины этих дефектов. Плоскодонные дефекты имеют равномерную глубину: 20%, 50%, 80% и 90%, где L = от 1 мм до 100 мм. Обнаружено, что от 100 мм и до 200 мм, амплитуда MFL сигнала относительно постоянная.

Когда L превышает 40 мм, соответствующий уровень размаха амплитуды (от пика до пика) приближается к форме плато, делая определение глубины в этой зоне проще и надёжнее. Амплитуду MFL сигнала при L менее 40 мм сложно использовать для определения глубины дефекта, что соответствует наблюдениям Марино и Друри [25]. Причина, по которой выявление дефектов малой длины сложна – это небольшой между двумя краями дефекта участок сопротивления наведённому магнитному полю. Чем ближе края дефекта друг к другу, тем слабее сопротивление становиться, позволяя большей части магнитного потока напрямую преодолевать расстояние между краями дефекта, образуя меньшую амплитуду MFL сигнала в непосредственной близости от магнитного сенсора.

Переменчивость амплитуды сигналов, показанная на Рисунке 1(a), в зависимости от длины дефекта, подтверждается наблюдениями, сделанными Чарльтоном [4], утечка магнитного потока больше завесила от его площади (аналогично длине в двумерном измерении), чем от глубины. Так же похожие результаты были получены командой Дж. Ци [26], с ростом длины (дефекта), размах (от пика до пика) амплитуды MFL сигнала будет расти. Эти признаки, обнаруженные Чарльтом [4] и командой Дж. Ци [26] можно рассматривать только, как аналог отношения MFL сигнала на Рисунке 1(a), когда дефекты длиной менее 40 мм.

Рисунок 1(b) это график погрешности, который показывает разницу между фактической глубиной дефекта и глубиной, определённой по MFL сигналу. Вертикальная ось графика представляет потенциальный процент погрешности между измеренной по MFL сигналу и реальной глубинами дефекта. График погрешности приведён для дефектов, представленных на Рисунке 1(а) относительно их длины.

На примере позиции (i) погрешность оценки глубины дефекта длиной 10 мм и глубиной 90%. Из графика видно, что для выбранного дефекта погрешность оценки глубины по амплитуде от реальной глубины дефекта составляет 12%. Возможно, это не очень значительная ошибка, так как при оценке с погрешностью глубина дефекта составила бы 78%, что так или иначе всё равно должно подвергся ремонту. Однако, посмотрим на позицию (ii) – пример, который может привести к протечке продукта из резервуара, если вовремя не произвести ремонт. Длина дефекта на позиции (ii) 5 мм, а реальная глубина 90%. При оценке глубины по MFL сигналу с приведённой погрешностью глубина дефекта составит 58%. На позиции (iii) демонстрируется неизбежность протечку продукта из резервуара. Оценка глубины по MFL сигналу с учётом высокой погрешности, показанной на графике позволит заключить вывод о незначительном классе дефекта. При длине дефекта 1 мм и глубине 90% потенциальная погрешность составит 63%. То есть дефект, имеющий реальную глубину 90%, будет значительно недооценён. Измеренная глубина по амплитуде MFL сигнала составит 27%. Как видно потенциальная погрешность при оценке дефектов может быть весьма серьёзная, если для оценки использовать только амплитуда MFL сигнала. Таким образом, при известной длине дефекта в сочетании с традиционным измерением амплитуды MFL сигнала, графики на Рисунка 1(а) могут послужить в качестве опоры для снижения погрешности измерения глубины дефектов по MFL сигналам.

В следующем разделе показана опорная диаграмма для измерения дефектов, основанная на измерениях, представленных в текущем разделе. Целью опорной диаграммы является улучшение достоверности измерения глубины дефектов небольшой длины.

Опорная диаграмма для измерения дефектов

В этом разделе мы предлагаем усовершенствованный подход измерения глубины дефектов с помощью опорной диаграммы, цель которой – снизить погрешность измерения глубины дефектов с помощью метода MFL. Диаграмма создана с помощью симуляции, базирующейся на амплитуде MFL сигналов от дефектов из графиков Рисунка 1, где диапазон длин дефектов от 1мм до 100мм, а диапазон глубины от 20% до 100%.

Чтобы оценить глубину неизвестного дефекта, требуются извлечь два значения из соответствующего MFL сигнала: амплитуда MFL сигнала и длина дефекта (показаны на Рисунке 2). Измерение значения амплитуды MFL сигнала относительно несложно. По размаху амплитуды можно измерить длину дефекта, применив метод поперечного измерение по Зиберту и Сазерленду [7]. Оценим точность полученного значения длины.

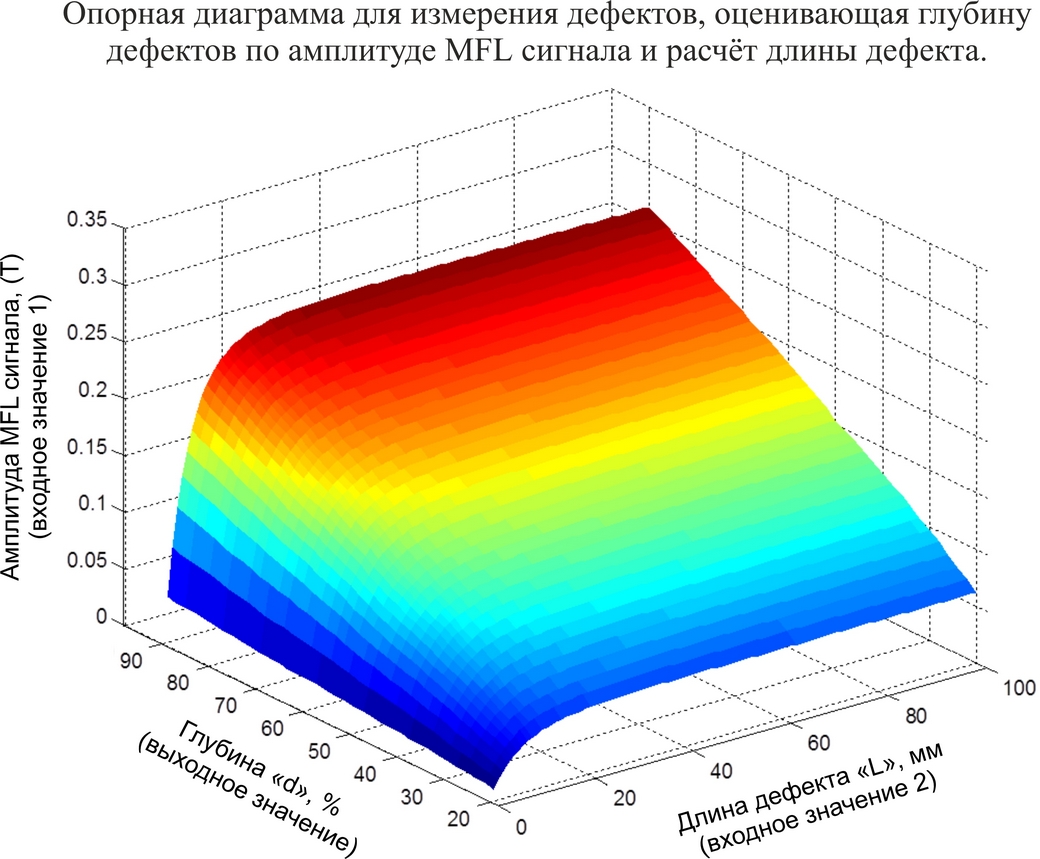
Рисунок 2. Это опорная диаграмма для измерения дефектов, которая может использоваться для определения глубины дефектов d по значениям, извлекаемым из соответствующих MFL сигналов: амплитуда сигнала и длина дефекта. Уровень амплитуды определяется по размаху отрицательного и положительного максимумов сигнала, а длину можно получить путём поперечного измерения размаха MFL сигнала.

Поперечное измерение размаха амплитуды показано на рисунке 3(а) посредством анализа погрешностей. Погрешность поперечного измерения размаха MFL сигнала показана, как зависимость от истинной длины дефекта. Длины дефектов, превышающие 8 мм, измерение размаха последовательно смещается на 2 мм. Это смещение может быть принято в качестве нормы. При длинах дефектов менее 8 мм погрешность увеличивается по мере уменьшения длины и может составлять 6 мм. Но если принять упомянутые ранее 2 мм смещения за норму, то впоследствии максимальная погрешность измерения длины дефекта уменьшается до 4 мм.

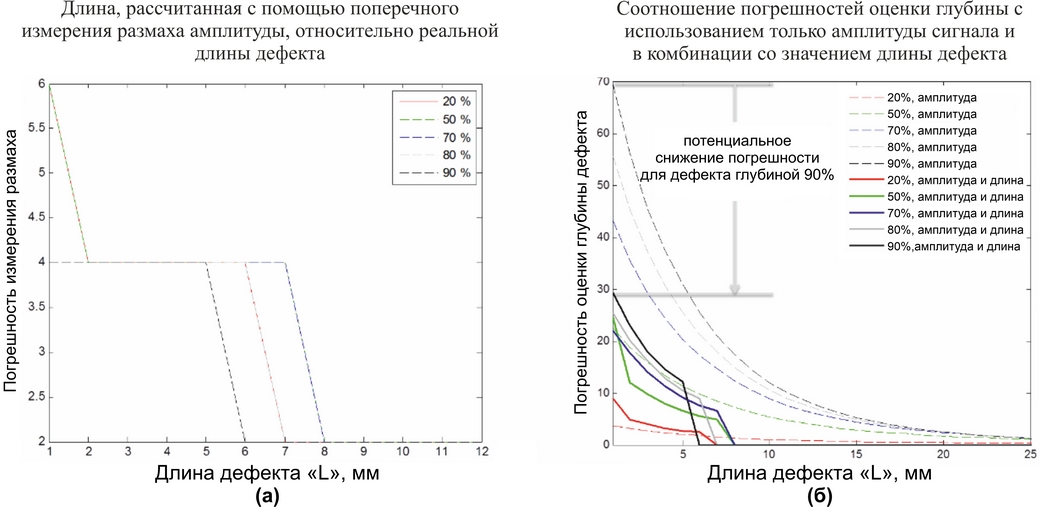
Рисунок 3(a). Анализ погрешности поперечного измерения размаха амплитуды MFL сигнала, предложенного Зибертом и Сазерлендом [7] для дефектов небольшой длины. Пять перекрывающихся графиков дефектов с глубинами 20%, 50%, 70%, 80% и 90% показывает двусмысленность при оценке глубины по размаху амплитуды. Когда дефект имеет длину, превышающую 8 мм, погрешность остаётся постоянной – около 2 мм. Рисунок 3(b) Погрешность в оценке глубины с помощью MFL сигнала относительно длины. Для удобства читателю, пунктирными линиями приводятся графики из Рисунка 1(b). Наблюдается снижение показателя погрешности при оценке глубины с включёнными параметрами амплитуды MFL сигнала, длины дефекта и настоящей опорной диаграммы для измерения дефектов. Напомним, что для измерения длины дефекта выполняется по размаху амплитуды в поперченном направлении.

Рисунок 3(b) показывает потенциальную погрешность оценки глубины по MFL сигналам дефектов с глубинами 20%, 50%, 70%, 80% и 90%. Каждый график построен относительно длины дефекта в диапазоне от 0 мм до 40 мм. Рассматриваются две погрешности: первая – при оценке глубины дефекта с использованием максимального значения амплитуды MFL сигнала, показано из Рисунка 1(b), а вторая – при оценке глубины с использованием опорной диаграммы для измерения дефектов. По пунктирным графикам на рисунке 3(b) видно, что погрешности особенно высоки для дефектов малой длины, что подтверждает сложность задачи точной оценки размеров, о чем сообщили Рамирес [12] и команда Дж. Ци [2]. Однако, используя значение амплитуды MFL сигнала дефекта, значение его длины и опорную диаграмму для измерения дефектов, можно значительно снизить погрешность (сплошные графики на рисунке 1(b)). Природа этого подхода основана на не очень точном измерении длины дефектов. Но даже с неточно измеренной длинной дефекта опорная диаграмма снижает погрешность измерения глубины дефектов примерно на 40%. Например, при измерении дефекта глубиной 90% и длиной 1мм, при измерении только по амплитуде MFL сигнала, глубина составит всего 27%, при использовании опорной диаграммы глубина составит около 63%. Данный подход, безусловно, требует дальнейшего изучения.

Заключение

Текущая практика быстрой оценки характеристик дефектов может быть выполнена с помощью опорных диаграмм. Одним из примеров опорных диаграмм для оценки дефектов коррозии это – диаграмма, основанная на взаимосвязи амплитуды MFL сигналов дефектов, которые равномерно растут, как по длине, так и по глубине, следуя тенденции равномерного развития коррозии. Но дефекты малой длины цилиндрической формы не демонстрируют равномерного роста, характерного для общей коррозии. По этой причине предлагается новый подход к опорной диаграмме для измерения дефектов, основанный на информации об амплитуде MFL сигнала и длине дефекта. Она может повысить точность измерения глубины дефектов.

В этой статье, поперечное измерение размаха амплитуды MFL сигнала, рекомендуемое Зибертом и Сазерлендом [7] принято для определения длины дефекта. В статье показано, что это не идеальный подход к измерению дефектов малой длины цилиндрической формы. Однако, предложенная опорная диаграмма может помочь существенно снизить погрешность при измерении глубины дефектов. Например, дефект глубиной 90%, при измерении существующим в практике способом. определяется как 27% глубины, а если применить предложенную опорную диаграмму, то измеренная глубина составит 63%. Это намного лучше, но безусловно требует дальнейших исследований в полях. Дальнейшее снижения погрешности измерений глубины дефектов требует более лучший способ измерения длины небольших дефектов формой близкой к цилиндрической. Предлагаемая опорная диаграмма для измерения дефектов является первым шагом. Она так же может включать дополнительные особенности дефектов, чтобы разработать более полную опорную стратегию.

Работа финансировалась компанией Silverwing UK Ltd

References

[1]D. H. Saunderson. The MFE tank floor scanner - a case history. IEE colloquium on non-destructive evaluation, 1988.

[2]J. Qi.  Experimental study of interference factors and simulation on oil-gas pipeline magnetic flux leakage density signal. International conference on mechatronics and automation, 2007.

[3]N. B. Cameron. Recommended practice for magnetic flux leakage inspection of atmospheric storage tank floors. Health and safety executive UK, 2006.

[4]P. C. Charlton. A theoretical and experimental study of the magnetic flux leakage method for the analysis of corrosion defects in carbon steel plate. PhD Thesis, Swansea institute of higher education, 1995.

[5]P. C. Charlton and J. C. Drury. The high speed inspection of bulk liquid storage tank floors using the magnetic flux leakage method. Insight, 35, No. 4:169–172, 1993.

[6]J. C. Drury. Magnetic flux leakage technology. Available at: http: //www.silverwing.com/ndt technical papers.aspx, (3/8/2011).

[7]M. A. Siebert and J. E. Sutherland. Application of the circumferential component of magnetic flux leakage measurement for in-line inspection of pipelines. NACE International, 1999.

[8]S. Huang, L. Li, H. Yang, and K. Shi. Influence of slot defect length on magnetic flux leakage. Journal of Materials Sciences & Technology, 20, 2004.

[9]J. Qi, S. Qingmei, L. Nan, Z. Paschalis, and W. Jihong. Detection and estimation of oil-gas pipeline corrosion defects. Proceedings of the 18th international conference on systems engineering (ICSE 2006), pages 173–177, 2006.

[10]S. Saha, S. Mukhopadhyay, U. Mahapatra, S. Bhattacharya, and G.P. Srivastava. Empirical structure for characterizing metal loss defects from radial magnetic flux leakage. NDT & E International, 43:507–512, 2010.

[11]A. R. Ramirez, N. R. Pearson, and J. S. D. Mason. An holistic approach to automatic classification of steel plate corrosion defects using magnetic flux leakage. 17th World conference on nondestructive testing (WCNDT), 25-28 Oct 2008.

[12]A. R. Ramirez. Automatic classification of defects in aboveground storage tanks via magnetic flux leakage. PhD Thesis, Swansea University, 2009.

[13]A. Sadr and S. Ehteram. Intelligent defect recognition from magnetic flux leakage inspection. The e-journal of nondestructrucive testing, May 2008.

[14]A. R. Ramirez, N. R. Pearson, and J. S. D. Mason. Automatic classification of defects in a corrosion environment. EUROCORR, 2009. [15]Y. Lijian, L. Gang, Z. Guoguang, and G. Songwei. Oil-gas pipeline magnetic flux leakage testing defect reconstruction based on support vector machine. 2nd International conference on intelligent computation technology and automation., 2009.

[16]P. Ramuhalli, L. Upda, and S. S. Upda. Neural network based inversion algorithms in magnetic flux leakage nondestructive evaluation. Journal of applied physics, 93(10), 2003.

[17]K. C. Hari, M. Nabi, and S. V. Kulkarni. Improved fem model for defect-shape construction from mfl signal by using genetic algorithm. Science, Measurement & Technology, IET, July 2007.

[18]M. Yan, S. Udpa, S. Mandayam, Y. Sun, P. Sacks, and W. Lord. Solution of inverse problems in electromagnetic NDE using finite element methods. IEEE transactions on magnetics, 34 (5), September 1998.

[19]C. Mandache and L. Clapham. A model for magnetic flux leakage signal predictions. Journal of Physics D: Applied Physics, October 2003. [20]M. Ravan, R.K. Amineh, S. Koziel, N.K. Nikolova, and J.P. Reilly.  Three-dimensional defect reconstruction from MFL signals using space mapping optimisation. 13th International Symposium on Antenna Technology and applied electromagnetics and the Canadian radio sciences meeting, 2009.

[21]X. Yuan, C. Wang, X. Zuo, and S. Hou. A method of 2D defect profile reconstruction from magnetic flux leakage signals based on improved particle filter. Insight, 53(3), March 2011.

[22]P. Ramuhalli, L. Upda, and S. S. Upda. Electromagnetic NDE signal inversion by function approximation neural networks. IEEE transactions on magnetics, 38, 2002.

[23]A. Joshi, L. Upda, S. Upda, and A. Tamburrino. Adaptive wavelets for characterising magnetic flux leakage signals from pipeline inspections. IEEE transactions on magnetics, 42, 2006.

[24]J. Fengzhu, W. Changlong, Z. Xianzhang, H. Songshan, and L. Siyang. LS-SVM based reconstruction of 3-D defect profile from magnetic flux leakage signals. Insight - Non-Destructive Testing and Condition Monitoring, 49(9), 2007.

[25]A. Marino and J. C. Drury. A comparison of the magnetic flux leakage & ultrasonic methods in the detection & measurement of corrosion pitting in ferrous plate & pipe. 15th World Conference on Non-Destructive Testing (WCNDT), 2000.

[26]F. Ji, C. Wang, S. Sun, and W. Wang. Application of 3-D FEM in the simulation analysis for mfl signals. Insight, 51 (1), January 2009.

• SliverWing_Practical limits of MFL in steel plate inspection

  pdf, 351 Кб